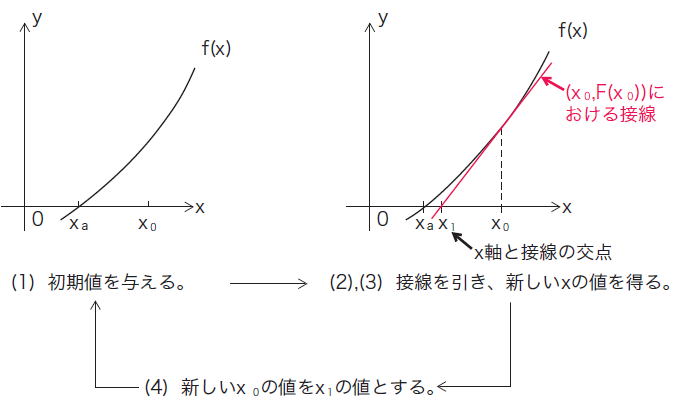
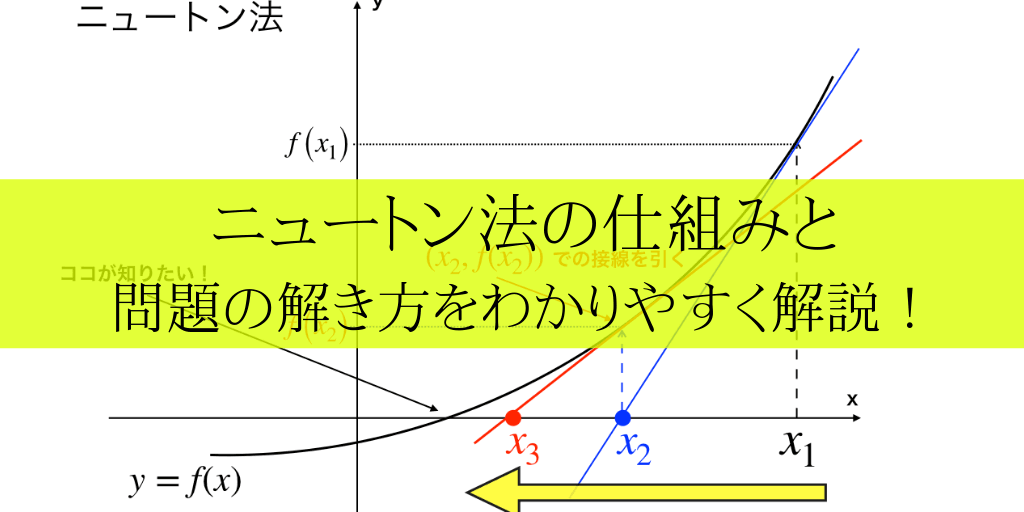
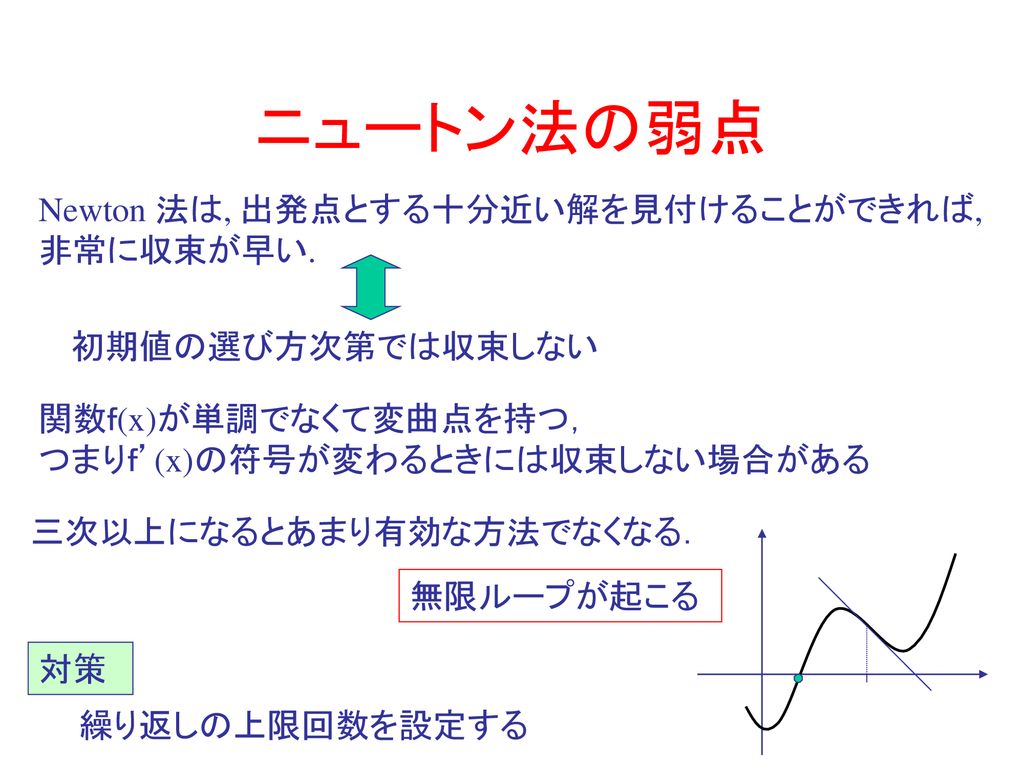
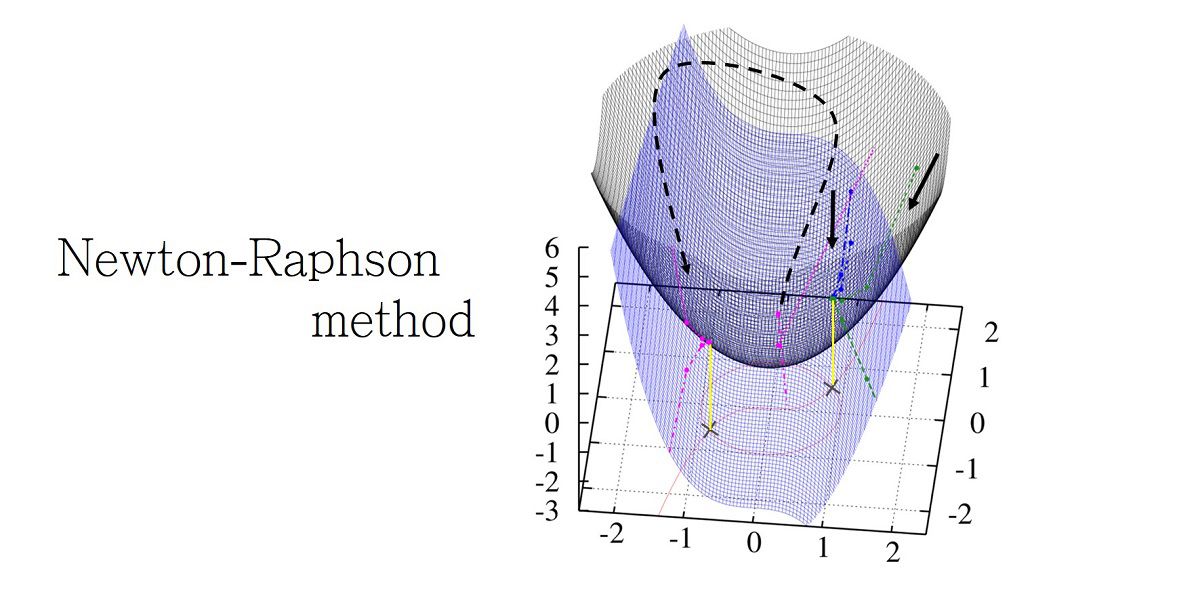
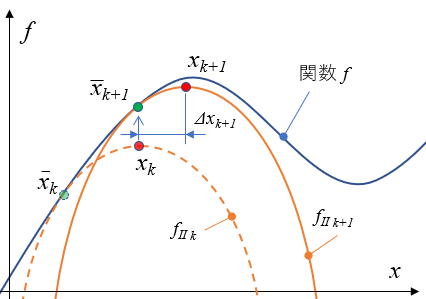
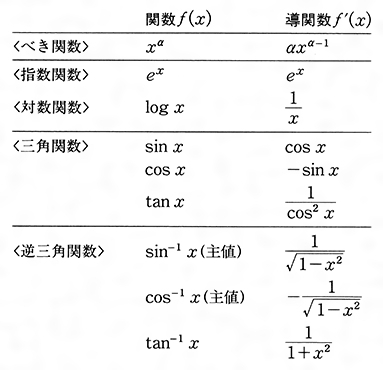
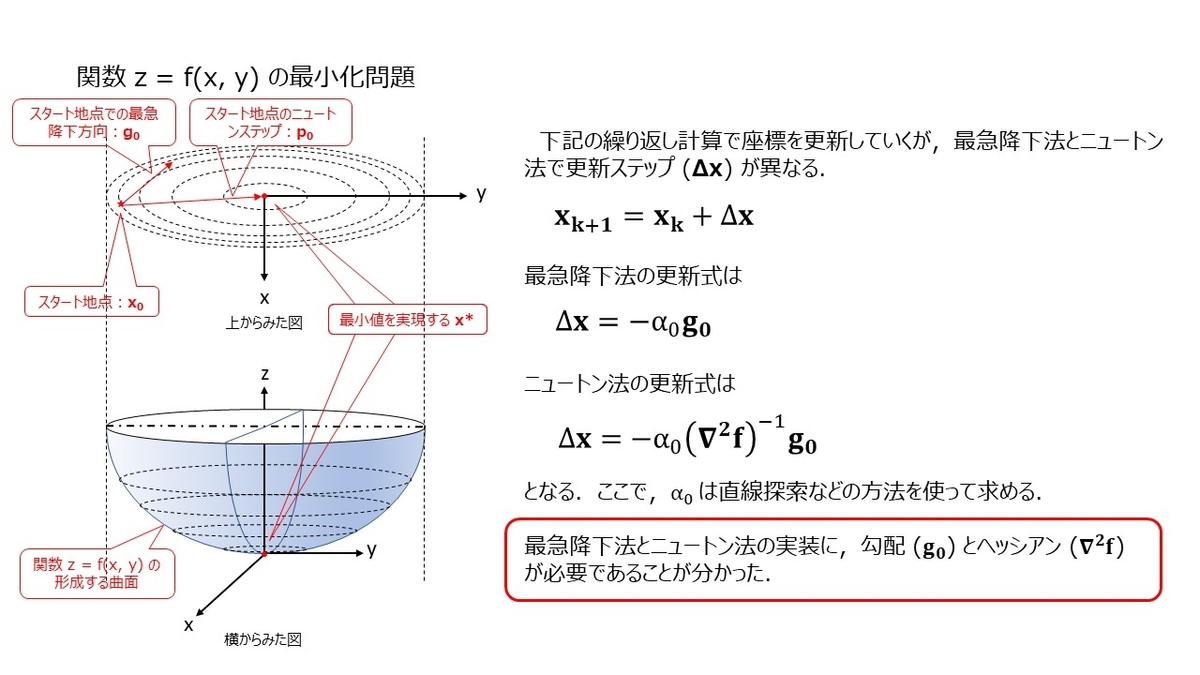
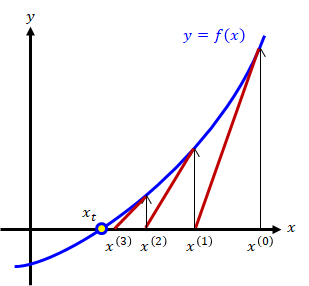
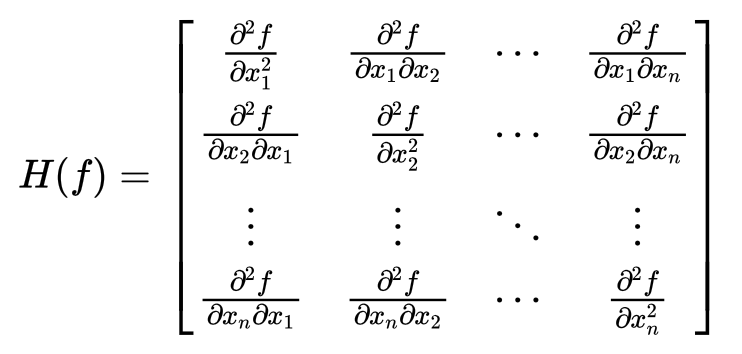
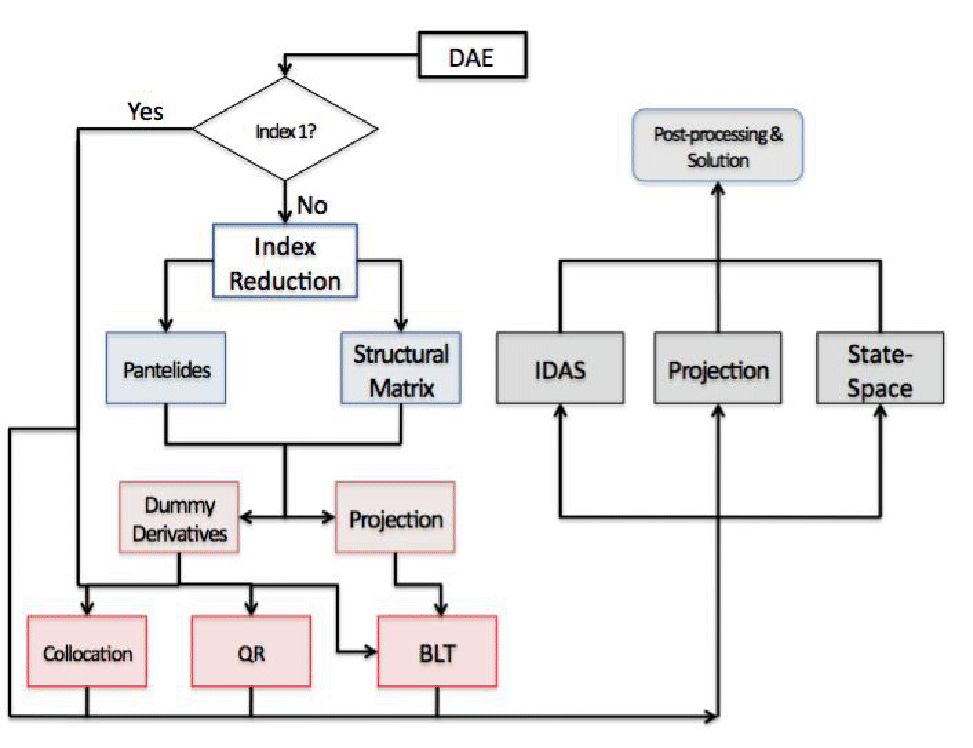
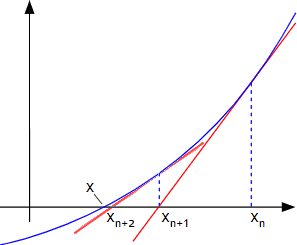
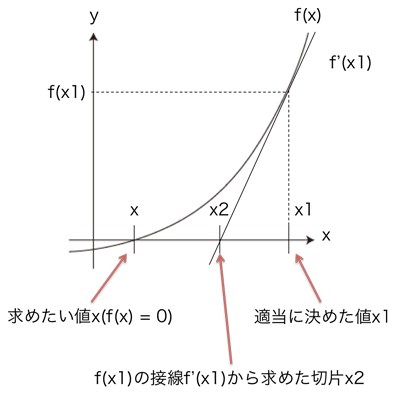
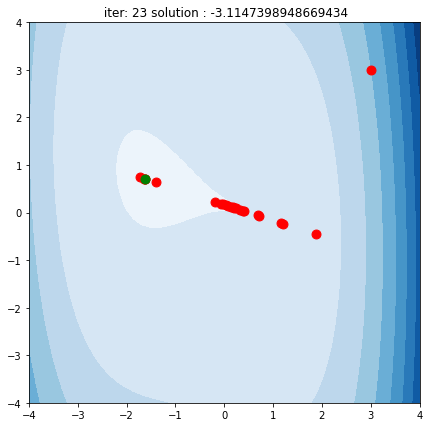
ニュートン法(ニュートン・ラフソン法) とは︖ 非線形方程式f(x) = 0 を数値的に解く方法の1つ 微分可能な方程式であれば、たとえ微分しなくても解が求まる 繰り返し計算により解に近づく 初期値を変えて何回か解く方がよい 1 問題設定 2 非線形方程式f (x) = 0 の解x を求める 曲線y = f (x) におけ
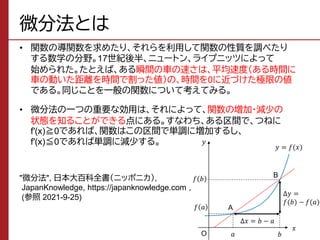
ニュートン 微分法- ニュートン法の原理 y = f(x)のように、任意の入力xに対し、関数値yが定まることがニュートン法を使える条件です。このとき、y = 0になるxの値を求めます。関数は微分可能であれば、ブラックボックスで構いません。 1642年(0才)ニュートン生まれる 1661年(18才)トリニティ・カレッジに入学 1665年(22才)微分法を発見。ペストの流行のため、故郷に帰る。 1668年(25才)反射望遠鏡を製作 16年(45才)国会議員になる 1717年(53才)イギリス政府、ニュートンの助言により1ギニー金貨=銀21シリングと定める
ニュートン 微分法のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | 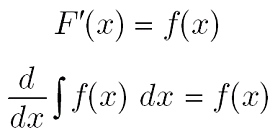 |  |
 | 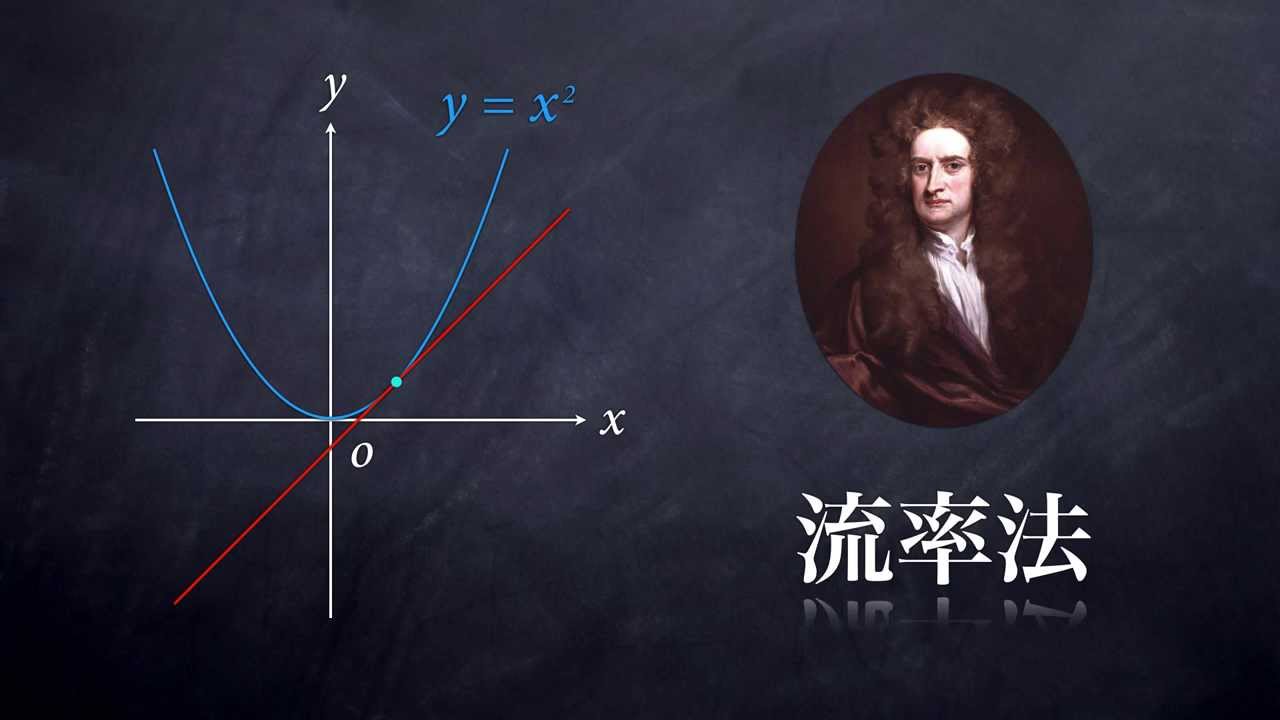 |  |
 | 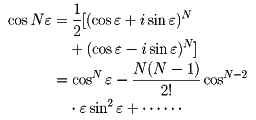 | 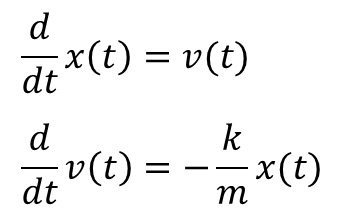 |
 |  |  |
「ニュートン 微分法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 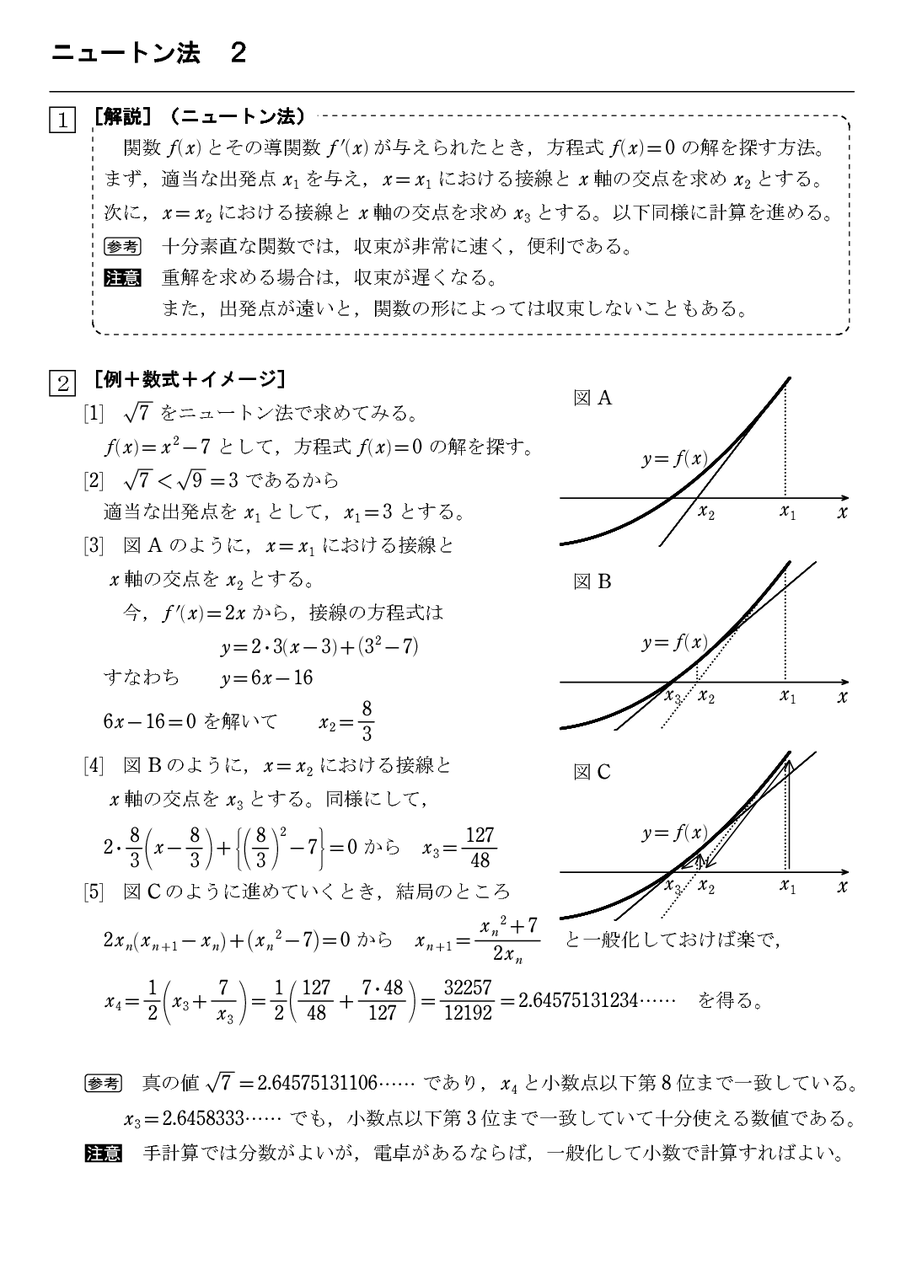 | 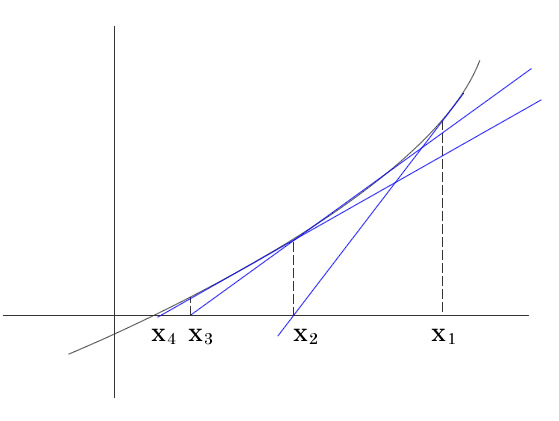 |
 | ||
「ニュートン 微分法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「ニュートン 微分法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「ニュートン 微分法」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  |  |
「ニュートン 微分法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 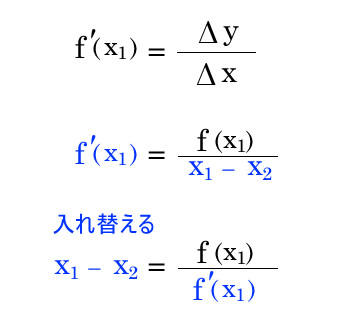 | |
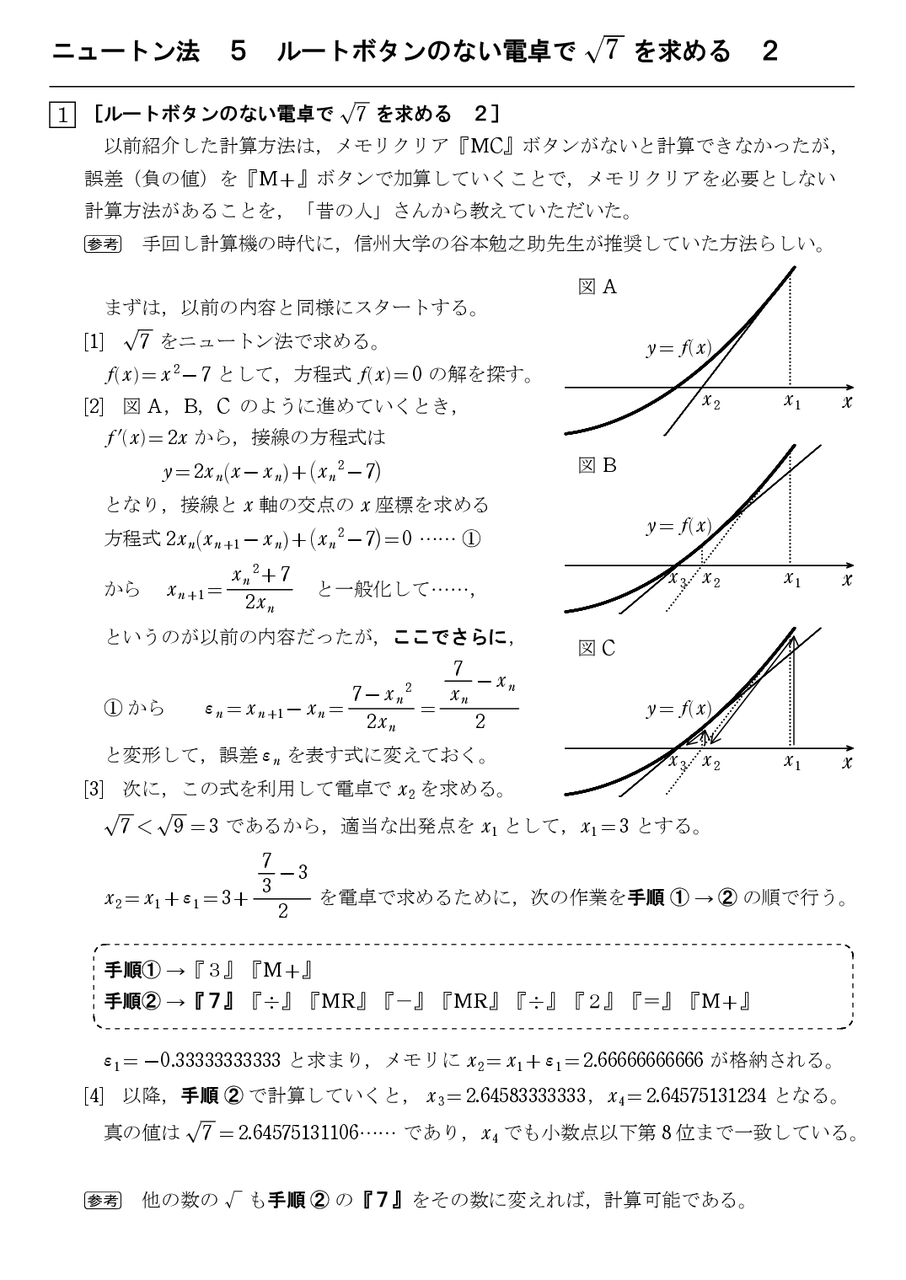 |  | |
「ニュートン 微分法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 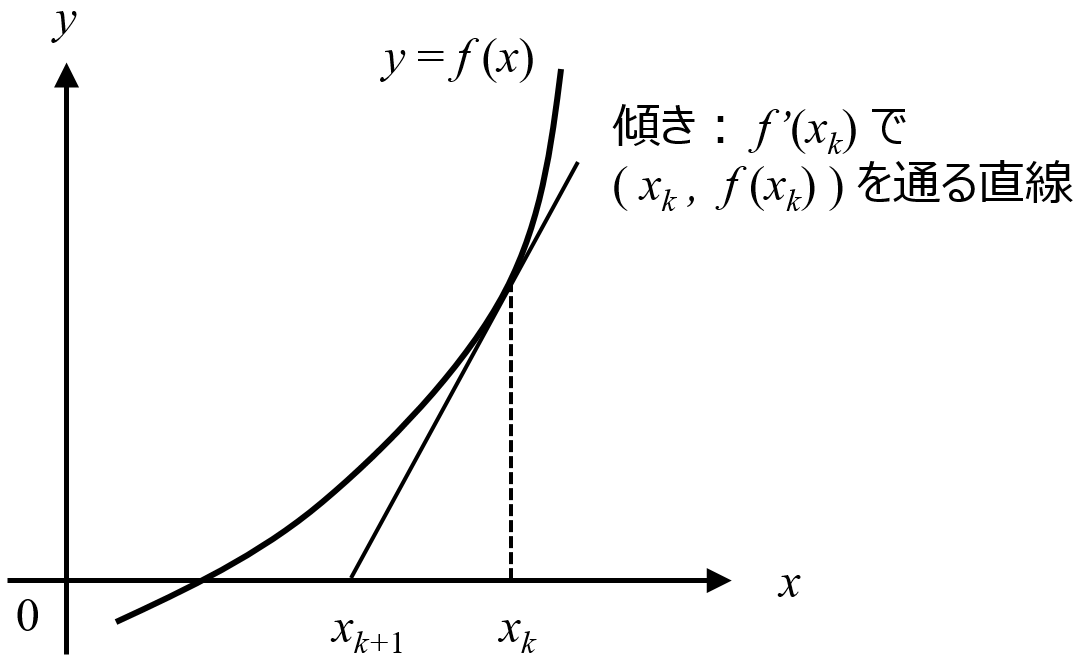 |
 |  |  |
 |  | |
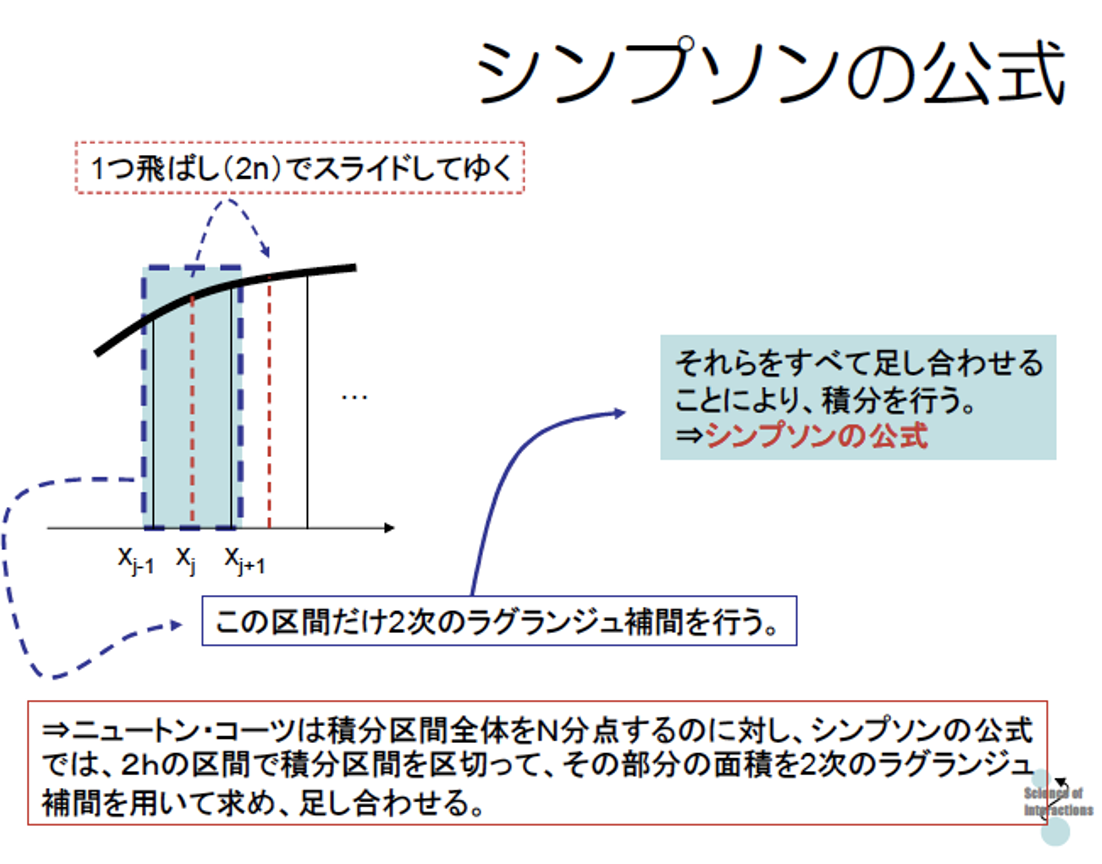 |  | |
「ニュートン 微分法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「ニュートン 微分法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 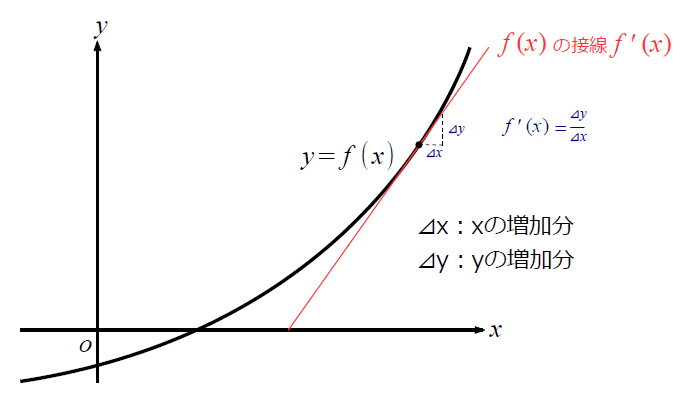 | |
 |  |
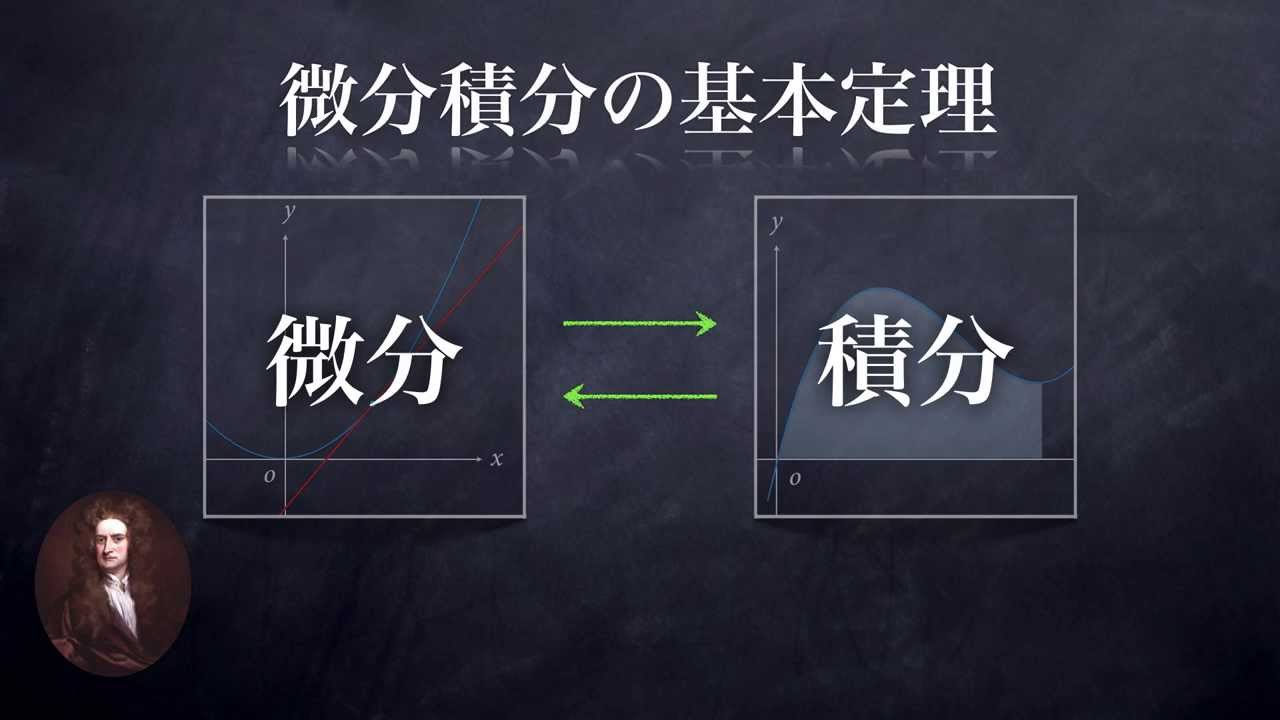
また、無限小の概念に基づく微分法発見。流率法の概念確立など次々と研究の成果を出す。 1668年(24歳) ニュートン式反射望遠鏡製作し、マスター・オブ・アーツとなる。 1669年(25歳) ケンブリッジ大学のルーカス教授に就任し、そこで光学を講義する。ニュートン方程式 十河 清 1 力学を学ぶ―私の経験から も同様で,微分法の性質(積の微分と合成関数の 微分)だけを使っており,具体的に微分を実行し ているわけではないからである。 そういう事情から,『力学i』では,力学と微分積 分を平行して導入することを主たる目標とし
Incoming Term: ニュートン 微分法,



